Exam 3

No lesson.

Graphing Lines

The equation of a line is

• x and y are the coordinates of any point on the line
• m is the slope (tilt) of the line
• b is the y-intercept (where the line crosses the y-intercept)

*Every line graphed on the coordinate plane is made up of at least TWO points.

In order to graph a line, you must need at least TWO points. Given the equation y = 2x + 3, you can set up a table to figure out the two points that you will need.

x	y = 2x + 3
0	3
1	5
2	7

Basically, choose any 3 values of x (you should start with 0 since that will give you the point for the y-intercept). Then, plug those values into the equation to figure out what the y-coordinates are for the given points.

Dilations

Dilation – is a transformation in which a given figure is enlarged or reduced.

Scale Factor – n determines the enlargement or reduction of the preimage.

If n > 1, then this indicates an enlargement

If n < 1, then this indicates a reduction

If n = 1, then the figure stays the same

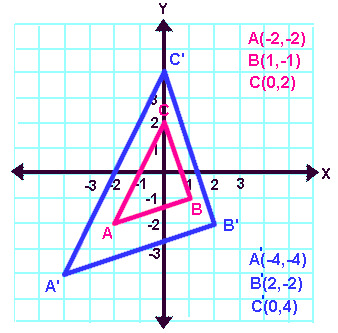
*The image of P(x, y) under a dilation in the coordinate plane with the origin as the center of dilation and a scale factor n is P'(nx, ny)

(x, y) –> (nx, ny)   – basically multiply each coordinate by the scale factor

ex: n = 3    (3, 2) —> (9, 6)

*To find the scale factor, you have to compute:

The x-coordinate of the image / the x-coordinate of the preimage

or the y-coordinate of the image / the y-coordinate of the preimage

An isometry is a transformation under which the image and preimage are congruent. Reflections, translations, and rotations are all isometries.

*A dilation is not an isometry

Translations and Rotations

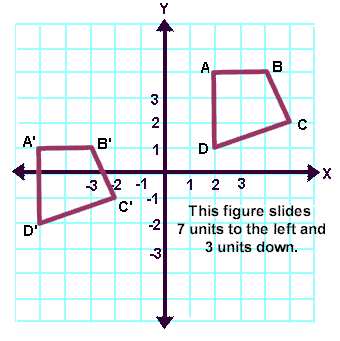
Translation – a transformation of a figure in which each point is moved the same distance in the same direction (also known as a slide).

*The image of P(x, y) under a translation a units horizontally and b units vertically is given by:

P(x, y) –>  P'(x + a, y + b)

**When you:

add to the x, you are moving to the right along the x-axis

subtract from x, you are moving to the left along the x-axis

add to the y, you are moving up the y-axis

subtract from the y, you are moving down the y-axis

Ex: translate P(-2, 4) to the right 5 units and down 3 units, the image will be:

P(-2,4) –> P'(-2 + 5, 4 + (-3)) = P'(3,1)

—

Rotation – a transformation involving turning of a figure or point.

We will only look at rotations about the origin. Memorize these:

*Rotation of 90° about the origin (x, y) –> (-y, x)

*Rotation of 180° about the origin (x, y) –> (-x, -y)

*Rotation of 270° about the origin (x, y) –> (y, -x)

Line/Point Reflections/Symmetry

In geometry, a transformation is the mapping of a figure, called the preimage, to a corresponding figure called its image. Both the preimage and image are congruent.

One type of transformation is called a line reflection. When you are only dealing with points, this is called point reflection.

Reflections across:

the x-axis (x, y) –> (x, -y)               the y-axis (x, y) –> (-x, y)

y = x (x, y) –> (y, x)                         origin (x, y) –> (-x, -y)

Note: the values of x or y don’t have to be positive. Do not get confused with the signs! For example, when you reflect (-4, -4) across the x-axis, you would get (-4, 4). Therefore, you are only changing the sign of the y-coordinate.

Notice how the coordinates of triangle A’B’C’ are the same coordinates as triangle ABC,BUT the signs have been changed. Triangle ABC has been reflected in the origin.

Line Symmetry – when a line of reflection creates two congruent parts

The Coordinate Plane, Average Rate of Change

The Coordinate Plane is made up of a y-axis (vertical line) and an x-axis (horizontal line).

The x and y axis intersect at a point called the origin.

*Every point in the coordinate plane has an x-coordinate (abscissa) and a y-coordinate (ordinate), such that point P(x,y).

*Any point that lies on the x or y-axis is not considered to be located in ANY quadrant.

Average Rate of Change

To find the average rate of change, divide the change in y by the change in x

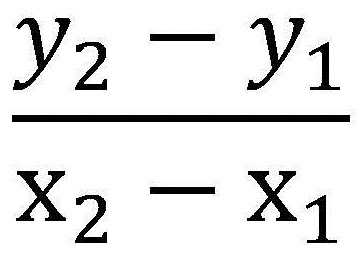
ex: On September 10 in midstate New Hampshire, the temperature at 6 A.M. was 45°F. At 2 P.M. on the same day, the temperature was 77°F. find the average rate of change in temperature per hour.

Hint: when you see the word per, it means divide. This tells you which variable is x and which is y.

77°F – 45°F / 2 P.M. – 6 A.M.

32°F / 8 hours = 4°F per hour

There was an average change of 4°F per hour.

Triangle Theorems

There are theorems (rules) that relate to triangles:

Triangle Angle Sum Theorem – the sum of the angles in a triangle is 180°

Triangle Side Sum (Inequality) Theorem – the sum of the lengths of any two sides of a triangle must EXCEED the length of the third side.

*If a, b and c are the lengths of the sides of a triangle and c is the largest side, then
(1) a²+ b² = c² => right triangle

(2) a² + b² > c² => acute-angled

(3) a²+ b² < c² => obtuse-angled

Exterior Angle of a Triangle

Transversals

Transversal – a line that crosses at least two lines

The red line is the transversal in each example:

Transversal crossing two lines	this Transversal crosses two parallel lines	… and this one cuts across three lines

When a transversal crosses the two parallel lines above, there are many different angles created.

Vertical Angles – are the angles opposite each other when two lines cross

In this example, a° and b° are vertical angles. *Vertical Angles are congruent: a° = b°

Corresponding Angles – are matching angles that are in the same position

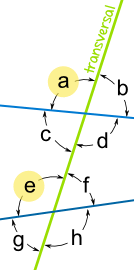
In this example, these are corresponding angles: a and e b and f c and g d and h *Corresponding Angles are congruent

Alternate Interior Angles – are angles that are opposite sides of the transversal, but inside the two lines

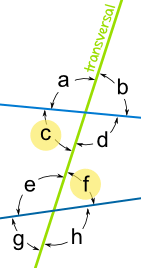
The pairs of angles on opposite sides of the transversal but inside the two lines are called Alternate Interior Angles. In this example, these are Alternate Interior Angles: c and f are Alternate Interior Angles d and e are also Alternate Interior Angles (To help you remember: the angle pairs are on “Alternate” sides of the Transversal, and they are on the “Interior” of the two crossed lines) *Alternate Interior Angles are congruent

Alternate Exterior Angles – are angles on opposite sides of the transversal, but outside of the two lines

In the example: a and h are Alternate Exterior Angles b and g are also Alternate Exterior Angles (To help you remember: the angle pairs are on “Alternate” sides of the Transversal, and they are on the “Exterior” of the two crossed lines) *Alternate Exterior Angles are congruent

Consecutive Interior Angles – are angles that are on the same side of the transversal and inside the two lines

In this example, these are Consecutive Interior Angles: d and f are Consecutive Interior Angles c and e are also Consecutive Interior Angles To help you remember: the angle pairs are “Consecutive” (they follow each other), and they are on the “Interior” of the two crossed lines *Consecutive Interior Angles are supplementary

Complementary Angles – angles that add up to 90°

Supplementary Angles – angles that add up to 180°

Squares and Square Roots, The Pythagorean Theorem

Squares & Square Roots

–          a² = squaring

*If a² = b, then a is called the square root of b

*PERFECT SQUARES are called “perfect”, because they have whole numbers as square roots. To find the square root of a number, think about which factor when multiplied by itself will give you that square. Ex: √64 = 8 because 8² = 64

*When finding the square root of a nonperfect square, you can approximate between two numbers. Ex: √28  –  this is between  √25 and √36, so your answer is between 5 and 6.

The Pythagorean Theorem

The Pythagorean Theorem states that: The square of the measure of the hypotenuse of a right triangle is equal to the sum of the squares of the measures of the two other sides.

Hypotenuse – the side opposite of the right angle

Simply, a² + b² = c²

or leg² + leg² = hypotenuse²

Using what we know about squares, lets see an example:

If a=3, b=4, find c.

a² + b² = c²

3² + 4² = c²

9 + 16 = c²

25 = c²

Something squared will give us 25. You can either guess and check, or you can find the square root of 25

√25 = √c²

5 = c

Sometimes, instead of being given the lengths of the two legs, you will be given the length of one leg and the hypotenuse.

Ex: If a=3, c=5, find b.

a² + b² = c²

3² + b² = 5²

9 + b² = 25

9 + b² = 25

9 + 16 = 25

√16 = 4

b = 4

Common Pythagorean Triples:

3:4:5   5:12:13   8:15:17   7:24:25   9:40:41

Types of Triangles, Similar Triangles

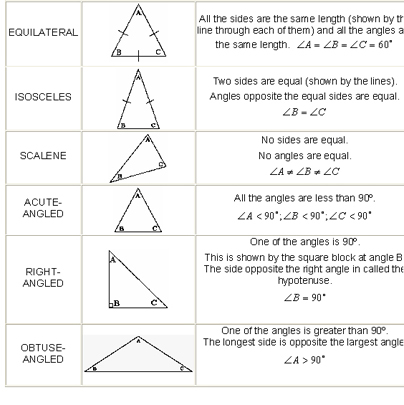
*Two triangles are similar if their corresponding angles are congruent

Similar triangles – triangles that have the same corresponding angle measures, but are different in length

Corresponding angles means angles that match up.

Corresponding sides of similar triangles have the same ratios.

Similarly, you can find the scale factor for each set of triangles by finding how much larger or smaller a triangle is multiplied or divided by.

To find the missing side of similar triangles, you have to set up a proportion.

10/x = 6/12   (find the cross products)

(10)(12) = (x)(6)   (simplify)

120 = 6x   (divide each side by 6)

20 = x